 |
|
|||
|
Hyperbolic Space online exhibit - Introduction Model galleries Press and other resources |
Hyperbolic
Space |
|||
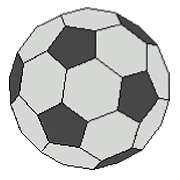
| For all its evident beauty and power, the Poincaré model of hyperbolic space is essentially an abstract construct. It obscures at the same time that it reveals, for we do not get a sense here of what it would feel like to be in hyperbolic space. By restricting ourselves to a Euclidean perspective we lose the visceral sense of hyperbolic being. Can we make a model of hyperbolic space that retains this physical sense - much as we have a visceral model of spherical space? For a long time mathematicians did not believe that such a model was possible. But it turns out there is a way of representing hyperbolic space that gives us a physical sense of at least some of its properties: the so-called hyperbolic soccer ball model. Think of a regular soccer ball: It is made up of hexagons and pentagons, with a series of white hexagons surrounding a smaller number of black pentagons. |
||||
 |
||||
| Hyberbolic soccer ball diagram by Brian McMullen, Cabinet magazine | ||||
Now think of the Euclidean plane (a regular flat plane). Here we can tile the surface with hexagons alone – the classic beehive pattern. |
||||
 |
||||
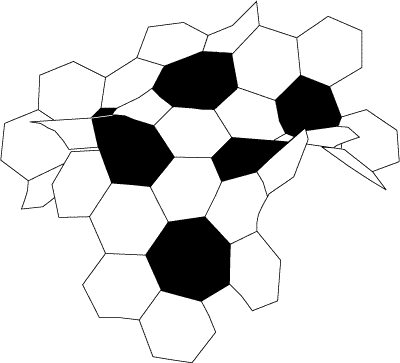
On the plane, every hexagon (which has six sides) is surrounded by six others and they all fit neatly together to exactly fill the space. To make a soccer ball, we replace some of the hexagons with pentagons (which only have five sides), thereby causing the now fewer number of hexagons to close up towards one another and wrap into a sphere. In the hyperbolic version of this model we make the opposite move. Rather than replacing some of the hexagons with pentagons, we replace them with heptagons (which have seven sides). Now, instead of closing up, the surface opens out – for the heptagons add to, rather than subtract from the space, and what we get is an excess of surface. The effect is similar to what we see in lettuce leaves and certain types of kelp where the vegetable surface expands outward from a modest start generating a ruffled effect. |
||||
 |
||||
| Download a pdf* to create a hyperbolic soccer ball | ||||
| Mathematicians now understand that lettuces and kelps are in fact natural examples of hyperbolic geometry - which is also found in the anatomical frills of sea slugs, flatworms and nudibranches. | ||||
 |
||||
| The hyperbolic ruffles of a marine flatworm. Photo by Ria Tan | ||||
| [ next ] | ||||
| © 2003–2018 The Institute For Figuring | ||||