 |
|
|||
|
Hyperbolic Space online exhibit - Introduction Model galleries Press and other resources |
Hyperbolic
Space |
|||
| To get to the heart of this enigmatic topic we must go back to Euclid and the original axioms of geometry. Long regarded as the model of intellectual rigor, Euclidean geometry is based on five supposedly self-evident propositions, or axioms. The first three are mundane enough: they define a line segment, an infinite straight line, and a circle. The fourth is also uncontroversial and states simply that all right angles are equal – a proposition necessary to ensure that the space we are working in is essentially the same everywhere. The property of sameness at every point is the defining quality of a geometry – for mathematically speaking there are wilder and more unruly spaces. Euclid’s fifth postulate also sounds entirely sensible: it defines the conditions for “parallel” lines. But from the beginning mathematicians sensed that this apparently reasonable proposition needed further investigation. There are several ways of describing this fifth, troublesome axiom, also known as the “parallel postulate.” Euclid’s own method is strange to modern eyes and mathematicians today prefer to use a construction discovered by the English mathematician William(TK) Playfair in the late nineteenth century. By Playfair’s description we may understand parallel lines in the following way:Imagine that I draw a line, and then define a point P outside that line. |
||||
 |
||||
| Fig 1a | ||||
| Now imagine that I draw various lines through the point P. What is the result? Euclid’s fifth axiom says that there is only one line I can draw through P that will never meet the original line. | ||||
 |
||||
| Fig 1b | ||||
All other lines would slant with respect to the original line and eventually intersect it. We call the non-intersecting lines parallels and denote them by little arrows, indicating that they continue on indefinitely without meeting. As stated above the parallel postulate seems intuitively correct. But it is so much more complicated than Euclid’s other axioms and from the beginning mathematicians felt haunted by the need for a less complex foundation. If this proposition is really true, they felt, then ought it not be provable from the other simpler axioms? That there is an issue here at all is suggested by the example of a sphere, whose surface forms another legitimate geometry. Again, we ask a question about the behavior of straight lines on the surface of a sphere. If we have a straight line drawn on a sphere and a point P outside this line (also on the sphere), then what happens when we try to draw other straight lines through the point P? |
||||
 |
||||
| Fig 2a | ||||
| Immediately we are faced with the question what does it mean to say a “straight line” on a surface like this that is curved? Mathematically, a straight line on a flat surface may be generalized to the concept of a geodesic, a term which can be defined as the shortest path between any two points. On the surface of a sphere the shortest path between two points is always along a “great circle” - a circle that divides the sphere into two equal halves, like the earth’s Equator. Airlines use such geodesics when charting the paths of international flights, which often look curved on a flat map but are in fact “straight” in relation to the globe itself. | ||||
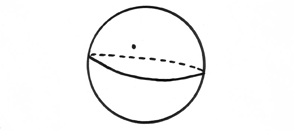 |
||||
| Fig 2b | ||||
| With respect to the sphere we notice immediately that the geodesics (straight lines) are not infinite as they are on a plane, but finite. They inevitably connect back up on themselves. Now returning to the initial question, we ask about the relationship between our original “straight line” and others we may draw through an external point P. | ||||
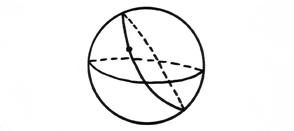 |
||||
| Fig 2c | ||||
Any straight line through point P is also by definition a great circle - and all great circles on a sphere intersect one another. Thus on the surface of a sphere there are no straight lines through a point that do not meet the original line. Where on the plane there was one line that never met, now we have a geometry in which there are none. How do we know that there may not be other options? For two thousand years mathematicians sought to prove that the parallel postulate must be true, in the sense that there could never be more than one straight line though a point that did not meet a given line. The idea that this might not be true struck terror into their Euclidean hearts offending rational sensibilities and evoking a sense of moral outrage. In order to prove the parallel postulate mathematicians resorted primarily to the method of reductio ad absurdum in which one begins by assuming the inverse of what ones hope to prove and then showing how this leads to a contradiction. That is, they assumed the parallel postulate was false and tried to show how that led inevitably to logical absurdity. What they discovered was a host of absurdities – but, infuriatingly, no outright contradictions. Girolamo Saccheri, an eighteenth century Jesuit priest who devoted his life to the problem of parallels, went to his Maker a failure in his own eyes, unable to demonstrate, after Sisyphean effort, a single contradiction. Finally, in the nineteenth century the effort to prove the parallel postulate exhausted itself, as mathematicians accepted the mounting evidence for the existence of a geometry based upon its absence. “I have created a new and different world,” Janos Bolyai wrote to his father in 1823. In Russia, Nickolai Lobachevsky came to a similar insight. An alternative to Euclid, however disturbing, was logically undeniable. To put it into Playfair’s terms, mathematicians were compelled to acknowledge that there exists a space in which given a line and an external point P, there are many lines that go through P yet do not meet the original line. |
||||
 |
||||
| Fig 3 | ||||
Instead of there being just one parallel to our original line, now there are many. Indeed there are infinitely many! Bizarre though it may seem, this situation gives rise to a consistent geometry, what came to be called, in homage to its abundant excess, hyperbolic space. At this point the viewer may object that most of these lines do not look straight. That is merely because we are trying to see them from our limited Euclidean perspective. From the point of view of someone within the hyperbolic space, all these lines would be perfectly straight and infinitely long and none would meet the original line. |
||||
| [ next ] | ||||
| © 2003–2018 The Institute For Figuring | ||||