Crocheting the Hyperbolic Plane:
An Interview with David Henderson and Daina Taimina
by Margaret Wertheim

This was first published in
Cabinet, Issue 16, Winter 2004

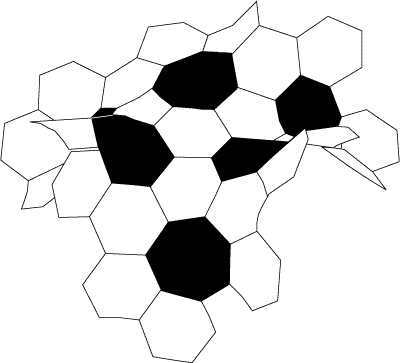
What exactly is a hyperbolic plane?

DH: There are many ways of describing the hyperbolic plane. In formal geometric terms it is a simply connected Riemannian manifold with negative Gaussian curvature. In higher-level mathematics courses it is often defined as the geometry that is described by the “upper half-plane model.” One way of understanding it is that it’s the geometric opposite of the sphere. On a sphere, the surface curves in on itself and is closed. A hyperbolic plane is a surface in which the space curves away from itself at every point. Like a Euclidean plane it is open and infinite, but it has a more complex and counterintuitive geometry.

The hyperbolic plane is sometimes described as a surface in which the space expands. Can you explain what that means?

DH: Actually that is true for many spaces, but it’s true for hyperbolic space in a particular way. Consider how circles on a surface behave. If you think of a series of circles around a point on a regular Euclidean plane, as you draw larger circles the length of the circumference increases linearly - by 2π times the radius or 2πr. Now on a hyperbolic plane, the circumference of the circles doesn’t just increase linearly, but exponentially. The perimeter and also the area of the circles gets bigger much faster. On a sphere, the circles get larger at first, but then as you go further they actually begin to get smaller. On a sphere the circumference of a circle is always less than 2πr, on a hyperbolic plane it is more. A similar thing happens with the area, which also increases much faster in hyperbolic space.

So as you move away from any point on a hyperbolic surface you get exponentially more space, so to speak.

DH: Yes, and you can get an idea of that with the hyperbolic soccer ball model that was discovered by my son, Keith Henderson A normal soccer ball has spherical geometry and is made up of hexagons and pentagons. Each pentagon, which has five sides, is surrounded by hexagons, which have six. If you just stuck together a lot of hexagons you’d get a plane, but in the soccer ball the presence of the pentagons pulls the hexagons away from flatness and the surface closes up on itself to form a sphere. To make a hyperbolic surface you replace the pentagons with heptagons, which have seven sides. Now you have to put in seven hexagons for every five you had before, so instead of closing up, the surface opens out and curves away from itself.

Why is the hyperbolic plane important historically?

DH: The discovery of the hyperbolic plane came from the attempt to prove Euclid’s fifth postulate, which is also known as the parallel postulate. For two thousand years mathematicians accepted this as true, but it had always caused problems.

DT: Mathematics is supposed to be an axiomatic system, but the fifth postulate does not look like an axiom, rather like a theorem. And so there were many attempts to try to derive the fifth postulate from the others. Nobody was able to do that. So the question eventually arose, well what happens if this postulate is not true? When mathematicians like Gauss and Bolyai and Lobatchevsky started to take that idea seriously, they discovered there was a geometry in which all of Euclid’s postulates hold true except for the fifth one.

Spherical geometry is pretty easy to understand because we see spheres all around us. But when mathematicians first started to study hyperbolic geometry they didn’t have any idea what this space might look like and they were nearly driven mad trying to understand this space. In 1997, Daina, you worked out how to make a physical model of the hyperbolic plane using crochet. How did that discovery come about?

DT: For the past 125 years or so mathematicians had conceptual models of the hyperbolic plane, such as the Poincare disc model, developed by the French mathematician Henri Poincare. Some of the models had great aesthetic appeal, especially through the enormous variety of repeating patterns that are possible in the hyperbolic plane. For instance, after the geometer Donald Coxeter explained these conceptual models to Escher, he used patterns based on these models in several of his prints.

But these were all conceptual models. Many students and mathematicians, including us, wanted a more direct experience of hyperbolic geometry - an experience similar to handling a physical sphere.

In 1868 the Italian mathematician Beltrami had described a surface called a pseudosphere, which is the hyperbolic equivalent of a cone. He actually made a version of his model by taping together long skinny triangles - the same principle behind the flared gored skirts some folk dancers wear. The in the 1970s the American geometer William Thurston had described another model of hyperbolic space that could be made by taping together a series of paper annuli, or thin circular strips. All these models were time consuming to make and hard to handle; they are fragile and they tear easily. I realized that Thurston’s construction could be made with knitting or crochet - basically all you’d have to do is increase the number of stitches in each row. I grew up in Latvia doing these handicrafts and I decided to try and make one. At first I tried knitting, but after a while you had so many stitches on the needles it became impossible to handle. I realized that crochet was the best method.

I have crocheted a number of these models and what I find so interesting is that when you make them you get a very concrete sense of the space expanding exponentially. The first rows take no time but the later rows can take literally hours, they have so many stitches. You get a visceral sense of what “hyperbolic” really means.

DT: We use these models a lot in our classes at Cornell. Most of our students don’t make the models themselves but they get a physical sense of the properties of the hyperbolic plane from studying them. One thing is that you can physically experience straight lines. You can fold the crochet models and see how straight lines behave and how they intersect. It really helps the students to understand very quickly the intrinsic properties of hyperbolic geometry.

DH: Another thing is that you can see the properties of triangles, particularly what’s called the ideal triangle. On a Euclidean plane the internal angles of a triangle sum to 180€, but on a hyperbolic plane they always sum to less than 180€. Moreover, as the vertices of the triangle get further away, the interior angles approach zero. When the points are at infinity, which is the largest triangle you can draw on the hyperbolic plane, the interior angles sum to zero. This is one of the exercises we give the students, and it’s very mysterious because the area of any ideal triangle on a hyperbolic plane will always be πr2, where r is the radius of curvature of the plane. So on any particular hyperbolic plane all ideal triangles are congruent - they all have the same area - which is pretty amazing I think.

What do other mathematicians think of this incursion of feminine handicraft into their domain?

DT: When they see the pictures in our book lots of people want to have models themselves. I’ve made them for mathematics departments all over the world. There is one in the Smithsonian in the American Mathematical Model Collection. But they are time-consuming to make and it’s tough on your hands because you have to hold the wool very tightly to get a good stiff tension with the crochet. These days people have to want one very badly and keep on calling me, then maybe I will make them one. In January 2005 at the Joint Mathematics Meetings in Atlanta there will be a special session on Mathematics and Mathematics Education in Fiber Arts in which I will be giving a talk on these models.

For a long time people thought that hyperbolic space was just some mathematical abstraction, but at the talk you gave at The Institute For Figuring you bought along a lot of hyperbolic lettuce leaves. We now that that there are actually lots of things in nature that exhibit this geometry - lettuce leaves, kelp and many different sea creatures, especially sea slugs, flat worms, and nudibranchs. Why didn’t mathematicians recognize this before?

DH: There were mathematicians who saw these things, but to think about them as a geometry – which is a very particular kind of structure - just didn’t occur to them.

DT: A lot of the more hyperbolic lettuce leaves are actually varieties developed for supermarkets, they’re not really the kind of thing you’d find much in nature.

DH: There are also not that many mathematicians sitting around looking at sea slugs. It’s only been fairly recently that mathematicians have been looking at things like leaves and trying to understand them. A lot of these can’t be understood in terms of analytic equations – neither can the physical model of the hyperbolic plane - so you have to use other kinds of methods, like geometric methods. It’s not until recently that we’ve had the tools to do that. One of the things that’s changing now is the advent of computers, which can help us to visualize mathematical objects. That is helping to bring back what’s called the “intuitionist” approach, which was there in the past but got blotted out by the “formalist” tradition for much of the past century. The formalists, wouldn’t accept anything unless it was expressed by equations.

Does that mean geometry is going to have some sort of renaissance?

DH: Oh yes, geometry is having a renaissance. One indication of this is the number of geometry courses being taught around the country. When I first came to Cornell there was only one undergraduate geometry course, now we have are eight A further indication is the work of another Cornell professor William Thurston, who has hypothesized a classification for the different types of three-dimensional manifolds – the three-dimensional analogues of two-dimensional surfaces (such as the surface of a sphere or a donut). Where two-dimensional geometry comes in just three types - the euclidean plane, the sphere and the hyperbolic plane - Thurston’s Hypothesis says that there are eight distinct 3-D spatial types. Over the past year the mathematical world has been excited by the news that Thurston’s Hypothesis might have been proved. If that turns out to be true then mathematics most famous geometric problem - the Poincare Conjecture - will also have been proved. which has a million dollar prize attached.

Apart from professional geometers, is there anyone else today who is affected by contemporary geometrical developments?

DT: Lots of other mathematicians are becoming interested in geometry to help with their own fields. Statisticians are especially interested.

DH: Statisticians often work with multidimensional spaces. They might have 123 dimensions of data they need to analyze, but in the end it’s a geometric object they are studying. Another place is in the movies. Pixar has some very good geometers working for them. Modeling fabric is one place where you need to have an understanding of curved space to simulate the drape of cloth and ruffles. Another example is in modeling skin. Some geometers are working on the problem of how to put a textured surface, which is already a geometric object, over an underlying structure, which is another geometric object. Auto industry engineers are also very interested in differential geometry, so they can design cars where the air flows smoothly around them, and acoustical engineers use my book on differential geometry to solve problems of sound design in concert halls.

One of the greatest problems in physics today is the question of what geometry our universe has. Is that something mathematicians can cast any light on?

DH: The indications are that the universe is close to flat, so most physicists think it’s close to Euclidean three space. But people with a geometric bent are saying there are different geometries that could also explain the observations. One potential geometry is a dodecahedral space, in which the basic symmetry of the universe is that of the dodecahedron (one of the five Platonic solids). This is something that geometers have been studying for a long time and there is some evidence that the universe has the properties that would fit this. A few years ago, some people were expecting the universe to be hyperbolic, but the evidence doesn’t seem to be pointing in that direction now. Data from NASA’s WMAP satellite may hopefully resolve this soon.

DT: If the universe has a dodecahedral geometry, it would be finite. Personally I’d quite like it if the universe were infinite and turned out to be hyperbolic. But it’s something to be determined by measurement. Poincare once wrote that no geometry could be considered more true than any other, only more convenient. Euclidean geometry is convenient, but that doesn’t mean it’s what nature uses.

See also:

A gallery of crocheted hyperbolic models

Download a pdf* to create a hyperbolic soccer ball

Lecture 02

Lecture 05

*pdf download requires Adobe Reader or Apple Preview