 |
|
|||
NEW + RECENT PUBLICATIONS
The Institute's first book, based on our Inaugural Lecture: // The IFF and cabinet Crystal Clear: An Interview with
Shea Zellweger The Mathematics of Paper Folding: Crocheting the Hyperbolic Plane:
|
Crystal
Clear: An Interview with Shea Zellweger This interview was first published in: |
|||
| In 1953, while working a hotel switchboard, a college graduate named Shea Zellweger began a journey of wonder and obsession that would eventually lead to the invention of a radically new notation for logic. From a basement in Ohio, guided literally by his dreams and his innate love of pattern, Zellweger developed an extraordinary visual system - called the “Logic Alphabet” - in which a group of specially designed letter-shapes can be manipulated like puzzles to reveal the geometrical patterns underpinning logic. Indeed, Zellweger has built a series of physical models of his alphabet that recall the educational teaching toys, or “gifts,” of Friedrich Froebel, the great nineteenth century founder of the Kindergarten movement. Just as Froebel was deeply influenced by the study of crystal structures, which he believed could serve as the foundation for an entire educational framework, so Zellweger’s Logic Alphabet is based on a crystal-like arrangement of its elements. Thus where the traditional approach to logic is purely abstract, Zellweger’s is geometric, making it amenable to visual play. Like his notation, Zellweger’s working methods are delightfully unconventional. While constituting a genuine research project in logic, his notebooks (made between 1953 and 1975) have remarkable visual appeal, passing through phases reminiscent of Russian Constructivism, outsider art, concrete poetry and pop. These days we accept outsider artists, and are perhaps aware of outsider scientists, but Zellweger may be the first we could define as an outsider logician. Although he has worked on the Logic Alphabet for over fifty years, his professional life has not been spent in departments of philosophy or mathematics, but in psychology, mostly at Mount Union College in Ohio, from which he retired in 1993. After half a century of obscurity, Zellweger’s work is starting to attract the attention of some mathematicians who believe it offers an exciting new perspective on logic. Christine Wertheim, co-director of the Institute For Figuring, has been studying Zellweger’s work, and talked with him about his unorthodox approach. | ||||

|
||||
| All images curtsey of Shea Zellweger | ||||
CW: The
history of logic is very interesting, and has undergone many phases.
In the Western world, it began about 2500 years ago when the Greeks
were developing a new form of civic structure in which debate and
argumentation replaced allegience to tradition as the major political
tools. Slowly philosophers realized that, if laws were to be based
on the outcome of arguments, an understanding of how valid arguments
are actually constructed was crucial. Formal logic began when thinkers
like Aristotle started using simple diagrams, like the famous Logic
Square, to study these structures. This was an amazing innovation
because it involved applying a mixture of algebra and geometry to
the study of language, that is, language in its role as the medium
of argumentation. During the middle ages, many thinkers dreamed
of being able to make a complete mathematical analysis of logic,
a complete formal notation for describing arguments and their components.
The Spanish nobleman Raymond Lull, a famous 11th century debaucher
who latter turned religious, was probably the first to have this
idea, and in that sense he is considered by some as the great-great-grandfather
of computing. However, the mathematization of logic didn’t
really get very far until the mid-nineteenth century when an Englishmen
named George Boole developed the first fully-fledged formal notation.
The study of logic radically changed at this point. It’s not
dissimilar to the way that in the sixteenth and seventeenth century
physicists revolutionized the study of motion by mathematizing it.
In what way does your work relate to this innovation? |
||||
 |
||||
| CW:But why do you need to show
these patterns? Both people and computors are doing fine using only
three or four connective-symbols, and not having a clue about the
lovely patterns hidden below. Why do you think it’s so important
to reveal these? SZ: It’s a bit like cladding a house in glass so you can see how it’s actually built, rather than covering it all in plywood and stucco which hides the underlying structure. To me it’s important not to just be able to do something, like driving a car. I also want to know how the thing works. In my notation, you could say that the design puts what’s under the hood onto the dashboard, so you learn how the vehicle works while you’re actually driving it. This makes the whole act of driving much less passive, and ultimately much more satisfying. I also like the fact that one’s interaction with my notation is literally hands-on and physical, rather than just all in your head. Knowledge shouldn’t be disconnected from the body. The body should be used as much as possible as a part of the means through which we acquire and store knowledge. Why can’t logic be like that too? CW: Does this mean that your notation offers not just a new kind of logical notation, but a whole different mindset – a new perspective really on what logic is. SZ: It is a different mindset, but what’s really important is how this approach plays out in the teaching of logic For most people, if they have encountered logic at all, it has probably seemed complicated, difficult, and full of abstract rules and symbols. My system is like a game whose simple and explicitly exposed structures enable you to easily understand the basic principles of logic, and even to begin doing some elementary constructions without learning any complicated rules. This is because the geometrical model on which it’s based can easily be embodied in objects you can manipulate with your hands and eyes. In fact, you can just play with the system as an interesting set of patterns in its own right. By flipping and rotating the elements you can explore the symmetries embedded in the system without seeing it as a way of modeling logic. CW:Your notation is specifically designed then to make these symmetry patterns tangible? SZ: The Logic Alphabet is a very special kind of writing that uses 16 letter-shaped symbols whose forms have been carefully designed to mimic the geometrical patterns underpinning logic. In many ways, it’s more like a pictographic language than a phonetic or purely abstract one. However, the pictorial aspect doesn’t just lie in the shapes of the individual symbols but also in the relations between them. What is important is the way you can turn one letter-shape into another by flipping and rotating, and that you can literally see this when you do it. Can you give me an example? SZ: For instance the Logic Alphabet includes the symbols ‘d’, ‘b’, ‘q’ and ‘p’. If you flip the d-letter to the right, it turns into a ‘b’. If you flip it upside-down it turns into a ‘q’. If you do both together, it rotates into a ‘p’. The other symbols in my Alphabet are also related by very specific symmetries which can be described by flips and rotations, and together all 16 form a pattern you can have great fun with. But it’s easier to grasp if you look at a three dimensional model first. CW:You built some models specifically for this purpose didn’t you? SZ: Yes. The Logic Alphabet is a script designed to be written on paper, so it’s only in two dimensions, but the overall patterns it captures are actually in four dimensions. Of course, we can’t build anything in four dimensions, but there is a three dimensional version that neatly encapsulates the basic figures. In the 70s I built some models as teaching tools, which beginners can play with. In this way they become familiar with symmetry and the beautiful patterns, long before they are able to think about logic itself. CW: In this sense your whole approach is similar to the ideas developed by the great nineteenth and early twentieth century pedagogues Friedrich Froebel and Maria Montessori, who founded the Kindergarten movement and the Montessori school system, respectively. Both believed that higher-level conceptual thought should be preceded by concrete hands-on play with geometric forms embodied in solid materials. SZ: That’s right. The whole way logic is taught today, as a system of purely abstract signs that only college-level students can understand, is completely backward. The Froebel-Montessori method of acquainting children first with fundamental patterns, and then later putting letters and other symbols on to these to show how the same forms are embodied in natural phenomena and geometric figures is exactly right. I’ve just extended this methodology to logic. In fact I think of myself as a Froebelian logician rather than as an outsider, because I think of logical structures as figures of thought, figures that can be explored materially. |
||||
 |
||||
| CW:You said
that the patterns underlying logic have a crystalline structure, and
that it is the symmetries of this crystal which your notation allows
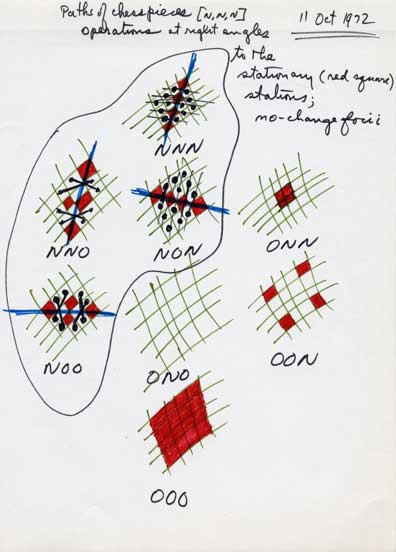
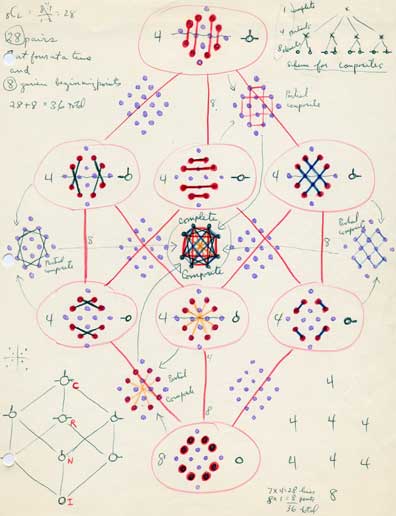
us to see and play with. Can you explain this? SZ: As I said when talking about the models, the Logic Alphabet is like a two-dimensional presentation of a higher-dimensional figure. The three-dimensional version of this figure is a Rhombic Dodecahedron, which is formed by the interpenetration of a cube and an octahedron. I call it the Logical Garnet because it looks like the gemstone Garnet. The letter-shapes of the Logic Alphabet were specially designed to make the symmetries embodied in this figure as easy to see as possible, and as easy to manipulate. |
||||
 |
||||
CW: We
don’t normally think of mathematical and logic notations as
works of ‘design’. We mostly assume that when a new
symbol is needed someone just makes it up without much thought about
its aesthetic qualities. At least, that’s what I thought until
I saw your work. CW:In the Logic Alphabet, all 16 connectives have their
own names, and each has a letter-shape as its symbol. I believe
you’ve devised a mnemonic to remember them by? |
||||
 |
||||
| SZ: It’s a
mini-drama with 16 letters and five acts about a man who keeps being
interrupted by his daughter’s noisy play. At first he tries
to persuade her to desist gently. When this fails he becomes increasingly
exasperated, and winds up ordering her out of the room altogether,
or leaving himself! I had to make up my own pronunciations for the
words beginning with the four nonstandard letters—–rAckett,
mIFty, rIFtee, yORders—–hence the increasing sense of
chaos and linguistic breakdown as the narrative unfolds. CW: You have said that dreams played a part in your logical research. Could you explain this? SZ: I’ve worked on this project a long time, so my mind keeps thinking about it, even when I’m doing other things. I never know when an idea will resolve itself, and when it does it can be at the oddest times, like in a faculty meeting. Once I woke up from a dream with an image of the letter ‘c’ on a swing spinning round and round. It gave me the solution to a problem I was occupied with at the time CW: You seem to have mostly been working alone... SZ: I don’t feel that I’ve ever really been alone. I have worked outside the fields of professional logic. I never taught it, nor even enrolled formally in any classes. I’ve pursued this thing in my spare time, and on the occasional sabbatical, but I was always able to find ‘soft spots,’ generous mathematicians who would from time to time listen to my ideas and give me help, especially the great geometer H. S. M. Coxeter, and my faculty colleague Glenn Clark. CW: In the 70s you took out patents on your ideas. Why did you do that? SZ: It was really an end run. Up to the mid-70s my papers always came back with rejection slips. So when I started making the models I figured that a record of my diagrams in the patent office would be at least one place where my work would be anchored publicly. You can’t patent ideas, such as logarithms, but you can get a patent on a slide rule, which is a material embodiment of them. My first patent was filed in October 1976, but not granted until June 1981. It was a long and torturous process. You have no idea! CW: Was it worth all the trouble? SZ: Absolutely. The specification included in each patent notes that my models are an “introduction to the crystallography of logic.” For me this was the first time that this expression has been used in print. This links logic to its deep roots in symmetry. CW: I believe your work is finally receiving some attention in the logical arena. SZ: No. Logicians aren’t interested at all. Unless you speak in their language they don’t want to know about your work. However, there are a few mathematicians who have taken an interest. You can find references to their papers on my web site at: www.logic-alphabet.net CW: Given how entrenched the logic world already is in its current notations, do you think your system, or something like it, will ever take off? SZ: Something like it, a notation of the same geometrical type as the Logic Alphabet. Yes, absolutely. I think it is inevitable. This is Froebel, Montessori, and Piaget all over again. Just give one generation of children the hands-on opportunity to play with models like mine in the early years of their cognitive development, and it could transform the way we do logic. |
||||
|
||||
| © 2003–2018 The Institute For Figuring | ||||