 |
 |
 |

|
 |
|
|
|
NEW + RECENT PUBLICATIONS
IFF PUBLICATIONs:

The Institute's second book is now available:
A Field Guide to Hyperbolic Space:
An Exploration of the Intersection of
Higher Geometry and Feminine Handicraft
by Margaret Wertheim
Based on the Institute's Inaugural Lecture:
The Figure That Stands Behind Figures
by Robert Kaplan
//
The IFF and cabinet
The institute has on ongoing relationship with Cabinet magazine
to publish in each quarterly issue an interview with one of our
speakers.
Things That Think:
An Interview with Computer Collector Nicholas Gessler
Cabinet issue 21
Where the Wild Things Are:
An Interview with Ken Millett
Cabinet issue 20
Evolving Out of the Virtual Mud:
An Interview with Ed Burton
Cabinet issue 19
Crystal Clear: An Interview with
Shea Zellweger
Developing the Logic Alphabet
Cabinet issue 18
The Mathematics of Paper Folding:
An Interview with Robert Lang
Cabinet issue 17
Crocheting the Hyperbolic Plane:
An Interview with David Henderson and Daina Taimina
Cabinet issue 16
|
Where
the Wild Things Are:
An Interview with Ken Millett
By Margaret Wertheim
This interview was first published in:
Cabinet, Issue 20, Winter 2005 |
 |
| A tight representation of knot
8.18 as rendered by Jason Cantarella with Ted Ashton, Michael Piatek
and Eric Rawdon |
| In mathematical lore,
a topologist is a person who cannot tell the difference between a
coffee cup and a donut, both objects being topologically the same.
Of the many things topologists strive to categorize, one of the more
enigmatic is knots. Though knotting is one of humanity’s oldest
and most widespread activities, at first glance it seems an unlikely
subject for the formalisms of mathematics. But at the end of the nineteenth
century, mathematicians began the task of classifying these twisted
and braided forms. Despite some initial success, by the 1960s knot
theory had reached a point of stagnation—many of the questions
being asked were simply too difficult to answer. In the 1970s, however,
knot theory was revitalized with the introduction of new analytic
methods and tools. In addition to theoretical advances, the insights
of knot theory are now being bought to bear on problems in biology
and chemistry, specifically to understanding the structure and behavior
of DNA, proteins, and polymers. Theoretical physicists studying subatomic
particles and forces also propose that the world is composed on knot-like
contortions in the substrate of spacetime. Ken Millett, a professor
of mathematics at the University of California, Santa Barbara, is
a leading knot theorist and a pioneer in the application of knot theory
to DNA. Millett is one of the co-discoverers of several classes of
“knot invariants,” polynomial equations used to classify
different knot types. His research interests include polygonal modeling
of knots, the spatial characteristics of physical knots, ideal knots,
and measures of complexity in knotted DNA. Millett is also a leader
in the field of mathematics education and is actively involved in
math outreach to minority communities in southern California. In November
2005, he gave a talk at the Institute For Figuring in Los Angeles—before
which he was interviewed by IFF director Margaret Wertheim. |
 |
Knot
images: courtesy of Eric Rawdon and Michael Piatek
(created using KnotPlot, a program for visualizing and exploring knots
by Rob Scharein) |
MW: How
did mathematicians become interested in knot theory?
KM: My understanding is that the mathematical origins came roughly
with the studies of Carl Friedrich Gauss (1777-1855) involving electromagnetism
and what would happen when an electric current is flowing through
a wire. That would depend upon the configuration of the wire in
space. That led later to the work in England of Lord Kelvin and
Peter Guthrie Tait at the end of the nineteenth century. They were
really the first to set about classifying configurations of knots,
in part because they believed that atoms might be knots in the ether.
MW: Why did anybody think knot theory had application to atoms?
KM: At the end of the nineteenth century, scientists realized the
world of knots was a discrete world, that is, different knot types
could be distinguished from one another. This raised the question
of whether knots were a good model for atoms, which seemed to have
a similar character - there are hydrogen atoms and oxygen atoms
and carbon atoms and so on, each with its own characteristics. In
fact there’s a continuing interest in this kind of discussion
today with string theory that also relates basic particles to complex
knot-like configuration.
MW: How do mathematicians go about formalizing something like tying
bits of string?
KM: Because it’s a human endeavor, the initial efforts were
kind of intuitive. In order to capture knotting in a piece of string
for example, it’s necessary to take the two ends and bind
them together so that you have a closed system. If you don’t
do that, you could move the knot off the end, making it disappear
as it were. The first questions that arise for mathematicians are
basic questions, such as: What does it mean to think of two knots
as the same or different? That’s a fundamental question that
would separate notions of topology from geometry, and you would
get a different answer depending on what kinds of equality or similarity
or equivalence you chose. Once you have that, then the question
comes as to the size of the population: How many different knots
are there? How would you distinguish between two instances of the
same knot in different forms? The mathematics comes with trying
to create a system and a process for identifying whether or not
two knots are equivalent. And also from the desire to establish
a complete classification, much as you would do with animals or
other things in science. Mathematicians want a complete classification
and we’re still struggling with ways in which to do that effectively.
|
 |
| All possible prime
knots ranging from 3:1 to 9:49. Diagrams by Ali Roth/Cabinet, from
Knots and Links by Dale Rolfsen (Publish or Perish Press, 1976). |
MW: The
population of possible knots is infinite, but how far have mathematicians
gone in terms of classifying them? And how do you gauge how far
you’ve got?
KM: In mathematics, the issue of “how far along you might
be” is a very sophisticated question. We know lots of different
ways of organizing information about knots. Since it’s a multidimensional
enterprise, it’s hard to say how far we’ve got because
from some perspectives we’re doing quite well, but if you
change the question a little bit, then we’re not doing so
well. If you organize knots, as was done classically, in terms of
their pictures or diagrams, and you judge complexity in terms of
these diagrams, then we’re not doing well. The classical way
of studying knots is to project an image of each knot onto a wall,
which reduces it to a planar diagram. When you do that, you see
a bunch of under- and over-crossings of string within the knot.
Now mathematicians say we should look at the picture with the fewest
number of these crossings, what we call the “crossing number.”
Looking at knots this way, we’re up to seventeen crossings.
Even at this level there are enormous numbers of possible knots—(for
seventeen crossings, we believe the number to be 8,053,249) The
computational task of going beyond that is formidable, and I’d
have to say that methods we have for distinguishing different knots
at this level are really quite primitive. As you increase the number
of crossings, it becomes exponentially more complex and at some
point becomes computationally intractable.
MW: Can you explain how mathematicians try to distinguish between
different knots?
KM: Aside from the crossing number, which is one feature, another
measure is to look at how you can model a knot with the smallest
number of line segments or edges. This is called polygonal modeling.
You can think of this as taking a segmented ruler, like a carpenter’s
rule, and bending it around to form a knot. Now we can ask: Can
you model a knot from four edges? It turns out you can’t.
The simplest knot is the trefoil or cloverleaf knot, and it takes
six edges to model that. All knots can be modeled from some number
of edges—this is what a lot of my work has been about recently—and
the question is, “How many edges do you need to represent
any particular knot?” That’s another measure. Another
one is to imagine that your knot is inside a sphere. For mathematicians
that’s not a very exotic task. Now take the “complement”
of the knot—that is the part of the space that’s not
the knot. In effect you’ve hollowed out the core of the sphere
and created a knot-shaped hole in it. For all except a well-understood
family of knots, this complement space can be given a hyperbolic
structure and associated with that is a hyperbolic volume. This
volume is another measure of the knot.
I should also mention another approach I’m partly responsible
for. There are certain algebraic or polynomial equations that we
call “knot invariants” that are associated with each
different knot. In knot tables, you’ll see lists of numbers
that define these equations. For many knots this is the main way
we have of characterizing them. It’s a pretty chaotic system
with all these different properties—there are even more than
the ones I’ve just described—and it would be good if
we could identify which are the core properties from which the others
derive.
|
 |
|
Knot images (above): courtesy of
Eric Rawdon and Michael Piatek
(created using KnotPlot, a program for visualizing and exploring
knots by Rob Scharein) |
MW: There
are knots that are “wild” and others that are “tame.”
Can you tell us what a wild knot is?
KM: I would explain it by giving you an example and then saying,
“Think like that.” Imagine I take a bunch of beads and
we’re going to make a sort of necklace. Now take the first
bead and I tie a little trefoil knot inside it. Now next to that
I attach another bead, but this time with half the radius and inside
that I make a smaller trefoil knot. Then next to that I put yet
another bead with half the radius still. Now imagine I take an infinite
sequence of these beads, each one half the size of the one before,
and each with a tiny trefoil knot inside. At the end I wrap the
string around so it’s closed. What makes this a wild knot
is that it’s composed on an infinite sequence. This is actually
one of the simplest examples you could make. Another way of describing
a wild knot is that it can only be modeled by an infinite number
of line edges. The opposite of wild is tame, which means you can
build it from a finite number of edges, like the trefoil knot I
mentioned before. Wild means you can’t.
MW: Do wild knots exist in the real world?
KM: In the physical science world, wild knots never happen. The
reason is there’s a smallest scale at which you can do things.
For wild knots, you have to be able to go smaller and smaller, until
it’s infinitesimally small. But here’s another question:
A knot is a one-dimensional structure; do such things exist as two-dimensional
structures? It turns out the answer is yes. We can have what’s
called a “wild sphere.” There was confusion about this.
The mathematician who first wrote about it, James Waddell Alexander,
said, “No, it’s not possible.” Then later, in
1924, he published a rebuttal saying here’s an example—which
is now called Alexander’s Horned Sphere. Just as a wild knot
cannot be modeled with a finite number of line segments, Alexander’s
Horned Sphere cannot be constructed from gluing together finitely
many triangles. It cannot be triangulated—it’s an infinite
polyhedral object.
MW: Do wild things occur in all dimensions?
KM: I am embarrassed to say I don’t know for sure. I suspect
the answer is yes. I have some recollection that strange things
happen in higher dimensional space that might make things easier.
But let me tell you about another really charming problem. Imagine
that we’re going to make a knot out of a polygon with, say,
thirty-two edges. And we’re interested in what are the different
knot types you can make with thirty-two edges. There’s a kind
of space of them, a world of them, a population. And you can sample
from them, sort of interview each one and ask, “What kind
of a knot are you?” This is a very classical statistical kind
of problem: You have a population and want to identify the constituents.
We know there are a finite number of knots you can make with thirty-two
edges; what we don’t know is whether that number is 600, or
1,000, or 10,000. There is no mathematical theory yet that’s
even been able to give us a meaningful estimate.
MW: You must have an answer up to a certain number of edges?
KM: Eight. That’s all we know about right now. It turns out
nine is already too complicated. And even for eight edges, there’s
one case we don’t know for sure.
MW: For eight edges how many knots are there?
KM: For eight equal-length edges, there are eight or nine different
knots, apart from the “trivial knot,” and we don’t
even know whether it’s eight or nine.
MW: It seems extraordinary that something so simple could
be so difficult.
KM: It is humbling.
|
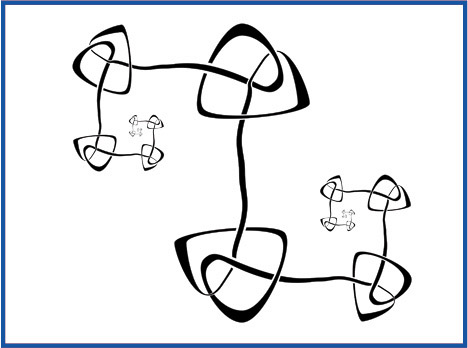 |
| Image
of a wild knot. |
MW: Can
you explain the idea that knots can be seen like numbers—you
can add them and subtract them, and there are even the knot equivalents
of prime numbers.
KM: That is a theorem that goes back to the 1960s. Remember how
we can construct a wild knot by making knots inside little beads?
Well, this method also tells you how to combine knots. If you take
one knot and put it inside a bead, and a second knot and put it
inside a bead, and so on to make a little necklace, that process
with some generalization also shows you how to take a knot and reduce
it into its atomic pieces—its indivisible parts. The way it
works is this: take a knot and let us try to find a sphere that
intersects with it at two points, so that inside the sphere is one
piece of the knot and outside is another. The technique tells us
that given any knot, however complex, we can find a finite collection
of spheres so that inside each sphere there is a piece of the knot
that cannot be broken down any further into simpler pieces. You
can move the spheres around so it looks like a chain of beads, each
with a little knot inside. Every knot is composed of a unique set
of these “irreducible” knots. It’s exactly like
building up composite numbers from prime numbers. These irreducible
knots are the primes of the knot world.
The unique factorization of knots is analogous to the unique factorization
of integers. With numbers, we call it multiplication, but with knots
we call it addition. One interesting thing about knots is that you
can never cancel out a knot by adding it to another knot.
MW: So there’s no knot equivalent of negative numbers?
KM: No there’s not. But it’s more accurate to think
in terms of reciprocals: If you take the number 2, then its reciprocal
is 1/2, and if you multiply 2 and 1/2 together, you get 1. The knot
equivalent of 1 is the trivial knot, or what is also called the
“unknot.” But you can never cancel out any knot and
get back to the unknot by adding it to another knot. There is no
such thing as knot reciprocals. |
 |
| Tight
representations of two knots rendered by Jason Cantarella with Ted
Ashton, Michael Piatek and Eric Rawdon. Ashton, Cantarellla, Piatek
and Rawdon developed an image animation program to simulate the process
by which knotted tubes tighten - the code for their program is called
RidgeRunner. These images depict the final sequence in the program,
the knot's final "tight" shape. |
MW: Knot
theory began out of an interest in electromagnetism and atoms, but
then it became pretty much a theoretical subject. Now it’s coming
back to applications. Can you comment on that?
KM: Knots have historical roots going back to the time people first
tried to attach things together using strands of fiber. We have pieces
of knotted material going back tens of thousands of years. The physical
properties of knots are very important for practical things like fishing
and hauling boats, but also because they occur in important biological
and physical systems such as polymers and DNA. This is what drives
a lot of my research now—the physical or spatial properties
of knots and their evolution in biological systems. DNA, RNA, and
proteins can be quite long structures and so their positions in space
can be quite complicated. If you take an electron micrograph of these
things, you will find lots of complicated structures and from a practical
point of view we’d like to be able to analyze that.
MW: Are pieces of DNA and RNA actually knots? Don’t knots have
to be closed?
KM: In nature there do exist DNA structures that are closed—these
are plasmids and they occur in viruses, etc. But it’s true that
a lot of DNA is open-ended. Some of the work I’m doing now is
to expand classical knot theory so that we can deal with the nature
of knotting in open strands. Here, we believe the critical thing is
to capture the nature of the knotting that occurs if you freeze their
position and we now have a pretty robust strategy for doing that.
Another example has to do with whether or not certain kinds of enzymes
can act upon DNA, whether they can access specific regions where they
could function and change the properties of the DNA. This is more
a geometric issue than a topological issue. It changes with the geometry
and flexibility of the materials. Why is this important? Well, some
structures are known to be critical in diseases like cancer, so the
ability to control those is a fundamental medical issue. There are
certain molecules, for instance, that have a part that’s hydrophobic
(water-hating) and other parts that are hydrophilic (water-loving).
The hydrophobic parts try to surround themselves so that they are
protected from the water by the hydrophilic parts. Now this material
is flexible, like a string of spaghetti, so one question is, “How
will that spaghetti organize itself?” How will it fold itself
up in space in order to best protect the hydrophobic parts? What are
the spatial properties of a configuration that does this best and
would there be knots in this structure?
MW: How
complex are DNA knots?
KM: For biological systems we are definitely interested in very large
knots. As we’re doing our analysis, I’ve got knots on
my computer with crossing numbers of 5,000. Those are pretty complicated. |
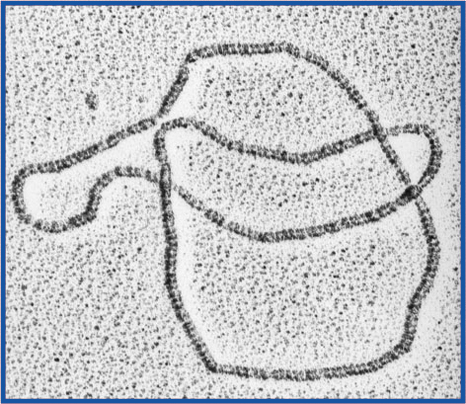 |
Electron micrograph
image of a protein-coated DNA trefoil knot. [Scale: 10 nanometers
diameter.]
Image courtesy of Andrzej Stasiak, University of Lausanne. |
MW: Does
it astonish you that we can start out with something as apparently
simple as a piece of string and 150 years later mathematicians haven’t
remotely exhausted what can be understood about that?
KM: As I look at the history of mathematics, there are many problems
we are only beginning to know how to ask, but we don’t yet have
the intellectual framework or tools to answer. The challenge often
is to figure out the questions where you can actually make progress.
That’s a real art form that successful mathematicians know how
to do. We learn how to ask questions for which we currently have a
hope of answering. We can work on impossible questions forever and
not get anywhere—the art is to ask those questions that we can
possibly answer.
MW: Do you see any questions in
knot theory being in the potentially impossible class?
KM: Certainly the classification of knots. I don’t think we
yet have the tools we need. It may be so hard that some people don’t
even consider it a legitimate question; it’s so far beyond what
they can even imagine doing. Personally, I think nothing is impossible,
it’s just a matter of time and imagination. |
|







